Answer:
Question 5.
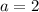
Question 6.
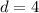
Explanation:
Question 5.
Given:
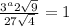
Solution:
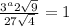

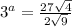
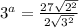
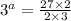
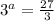
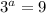

Take log both side.
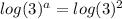
Simplify th above equation.
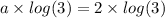
log(3) cancelled both side
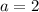
Question 6.
Given:
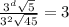
Solution:
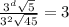
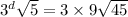
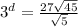
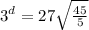
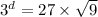
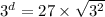
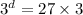
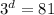
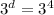
Take log both side.
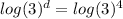
Simplify the above equation.

log(3) cancelled both side
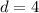
Therefore
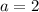 for question 5 and
for question 5 and
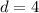 for question 6.
for question 6.