Question

Hello i need help on these two questions thank you

Answer 1

Question 5.
`a=2`

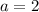
Question 6.
`d=4`

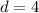
Explanation:

Question 5.

Given:

`(3^(a)2√(9))/(27√(4)) = 1`

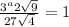
Solution:

`(3^(a)2√(9))/(27√(4)) = 1`

`3^(a) 2√(9) =27√(4)`

`3^(a) =(27√(4) )/(2√(9) )`

`3^(a)=\frac{27\sqrt{2^(2) } }{2\sqrt{3^(2) } }`

`3^(a)=(27* 2)/(2* 3)`

`3^(a)=(27)/(3)`

`3^(a)=9`

`3^(a)=3^(2)`

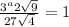
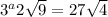
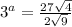
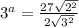
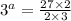
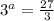
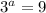
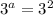
Take log both side.

`log(3)^(a) =log(3)^(2)`

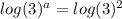
Simplify th above equation.

`a* log(3)=2* log(3)`

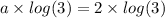
log(3) cancelled both side

`a=2`

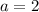
Question 6.

Given:

`(3^(d)√(5))/(3^(2)√(45)) = 3`

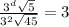
Solution:

`(3^(d)√(5))/(3^(2)√(45)) = 3`

`3^(d)√(5) =3* 9√(45)`

`3^(d) =(27√(45) )/(√(5) )`

`3^(d) =27\sqrt{(45)/(5)}`

`3^(d) =27* √(9)`

`3^(d) =27* \sqrt{3^(2)}`

`3^(d) =27* 3`

`3^(d) =81`

`3^(d)=3^(4)`

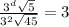
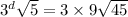
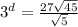
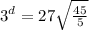
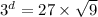
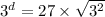
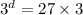
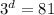
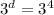
Take log both side.

`log(3)^(d) =log(3)^(4)`

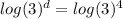
Simplify the above equation.

`d* log(3)=4* log(3)`

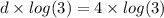
log(3) cancelled both side

`d=4`

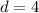
Therefore
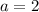`a=2` for question 5 and
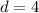`d=4` for question 6.