Question

A rectangular sheet of cooper is twice as long as it is wide. From each corner a 3-inch square is cut out, and the ends are then turned up to form a tray. If the volume of the tray is 324 cubic inches , what were the original dimensions of the sheet of cooper?

Answer 1

length=24 inches and width=12 inches

Explanation:

Let width of the rectangular sheet be x.

Then its length is twice as width = 2x

From each corner 3-inch square is cut to form a tray.

The length of the tray formed = l = 2x-6 (total length - length of 2 squares cut out from both ends)

The width of the tray formed = b = x-6 (total width - length of 2 squares cut out from both ends)

Height of the tray formed = h = 3 inches

Volume of the tray = l*b*h = (2x-6)*(x-6)*3 = 324 cubic inches.

`2x^(2)-18x+36=108\\x^(2)-9x-36=0\\(x-12)(x+3)=0\\x=12`

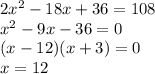
The length and width of the sheet is 24 and 12 inches respectively.