Answer:
length=24 inches and width=12 inches
Explanation:
Let width of the rectangular sheet be x.
Then its length is twice as width = 2x
From each corner 3-inch square is cut to form a tray.
The length of the tray formed = l = 2x-6 (total length - length of 2 squares cut out from both ends)
The width of the tray formed = b = x-6 (total width - length of 2 squares cut out from both ends)
Height of the tray formed = h = 3 inches
Volume of the tray = l*b*h = (2x-6)*(x-6)*3 = 324 cubic inches.
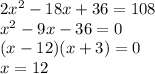
The length and width of the sheet is 24 and 12 inches respectively.