Question

If anyone could help I’d appreciate it! Thanks

Answer 1

0.72 sec

0.28 sec

Explanation:

Modeling with Functions

Scientists and mathematicians are always trying to find adequate models to approach to reality. It allows us to better understand the nature of the problems and gives us the opportunity to project its behavior to the future and make predictions

The ball's height h in meters after t seconds is modeled by the function

`\displaystyle h=3+5t-5t^2`

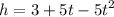
We are required to find all values of t for which the ball's height is 4 meters. We set the condition like shown below

`\displaystyle 3+5t-5t^2=4`

Rearranging

`\displaystyle 5t^2-5t+1=0`

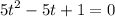
We need to solve the second-degree equation, which can be solved by using the formula

`\displaystyle t=(-b\pm√(b^2-4ac))/(2a)`

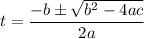
where a=5, b=-5, c=1

`\displaystyle t=(- (-5)\pm√((-5)^2-4(5)(1)))/(2(5))`

`\displaystyle t=(5\pm √(25-20))/(10)`

`\displaystyle t=(5\pm √(5))/(10)`

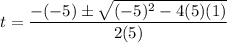
This provides two solutions

`\displaystyle t=(5+ √(5))/(10)=0.72\ sec`

`\displaystyle t=(5- √(5))/(10)=0.28\ sec`

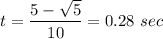
Both solutions are positive and therefore valid