Answer:
The measure of side MO is 8 unit
Explanation:
Given as :
In the Triangle ΔMOP ,
∠P = 90°
∠M = 60°
The perimeter of ΔMOP = 12 + 4√3
Now, From figure , in Triangle ΔMOP
∠O = 180° - ( ∠P + ∠M )
or, ∠O = 180° - ( 90° + 60° )
or, ∠O = 180° - 150°
∴ ∠O = 30°
Now, from Triangle
Sin 90° =
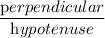
Or, Sin 90° =

Or,
 = 1
= 1
Again
Sin 60° =
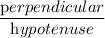
Or, Sin 60° =

Or,
 =
=
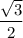
Similarly
Sin 30° =
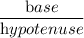
Or, Sin 30° =
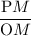
Or,
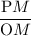 =
=

So, The ratio of the sides as
PM : MO : OP = 1 : 2 :

Let PM = x
MO = 2 x
OP = x

Now, from question
The perimeter of triangle ΔMOP = 12 + 4√3
I.e, The sum of sides of triangle ΔMOP = 12 + 4√3
or, PM + MO + OP = 12 + 4√3
or, x + 2 x + x
 = 12 + 4√3
= 12 + 4√3
or, 3 x + x
 = 12 + 4√3
= 12 + 4√3
Or, x ( 3 +
 ) = 4 ( 3 +
) = 4 ( 3 +
 )
)
Now, equating both side we get
x = 4
So, The measure of side MO = 2 x
I.e The measure of side MO = 2 × 4 = 8 unit
Hence The measure of side MO is 8 unit Answer