Answer:
6 and 7 are the consecutive numbers.
Explanation:
5 and 6 are consecutive integers because 6 is right after 5.
Let me revise the way I say that:
5 and 5+1 are consecutive integers.
So
 and
and
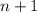 are consecutive integers.
are consecutive integers.
If they are both positive, then clearly
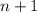 is more than
is more than
 .
.
We are given the square of the smaller,
 , is added to seven times the larger,
, is added to seven times the larger,
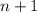 , is equal to 85.
, is equal to 85.
This means:
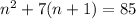
Let's solve.
First we should use the distributive property:

Now I would like the right hand side to be 0 so I can factor and then put both factors equal to 0 and solve for
 .
.
Subtract 85 on both sides:
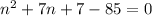
Simplify:
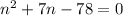
Now we want to find two numbers that multiply to be -78 and add to be 7.
Let's think of some numbers that multiply to be -78:
-78=-2(39); this wouldn't work because -2+39 isn't 7
-78=2(-39); this wouldn't work because 2+(-39) isn't 7.
-78=-6(13); this would work because -7+13 is 7.
So the factored form is:
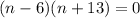
This implies
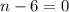 or
or
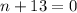 .
.
We are going to solve the first equation by adding 6 on both sides giving us:
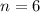 .
.
We are going to solve the second equation by subtracting 13 on both sides giving us:
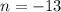 .
.
Now we are looking for positive integers, so
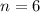 .
.
This implies the value of
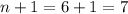 .
.
The numbers are 6 and 7.
Let's check.
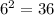 <-This is the square of the smaller.
<-This is the square of the smaller.
 <-This is the square of the smaller added to seven times the larger. We got 85 so the check is good.
<-This is the square of the smaller added to seven times the larger. We got 85 so the check is good.