Question

Find two consecutive positive integers such that the square of the smaller integer added to seven times the larger integer is equal to 85

Answer 1

6 and 7 are the consecutive numbers.

Explanation:

5 and 6 are consecutive integers because 6 is right after 5.

Let me revise the way I say that:

5 and 5+1 are consecutive integers.

So
`n` and
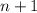`n+1` are consecutive integers.

If they are both positive, then clearly
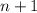`n+1` is more than
`n`.

We are given the square of the smaller,
`n`, is added to seven times the larger,
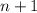`n+1`, is equal to 85.

This means:

`n^2+7(n+1)=85`

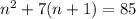
Let's solve.

First we should use the distributive property:

`n^2+7n+7=85`

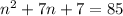
Now I would like the right hand side to be 0 so I can factor and then put both factors equal to 0 and solve for
`n`.

Subtract 85 on both sides:

`n^2+7n+7-85=0`

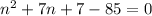
Simplify:

`n^2+7n-78=0`

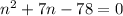
Now we want to find two numbers that multiply to be -78 and add to be 7.

Let's think of some numbers that multiply to be -78:

-78=-2(39); this wouldn't work because -2+39 isn't 7

-78=2(-39); this wouldn't work because 2+(-39) isn't 7.

-78=-6(13); this would work because -7+13 is 7.

So the factored form is:

`(n-6)(n+13)=0`

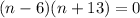
This implies
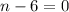`n-6=0` or
`n+13=0`.

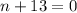We are going to solve the first equation by adding 6 on both sides giving us:
`n=6`.

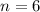We are going to solve the second equation by subtracting 13 on both sides giving us:
`n=-13`.

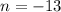Now we are looking for positive integers, so
`n=6`.

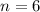This implies the value of
`n+1=6+1=7`.

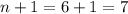The numbers are 6 and 7.

Let's check.

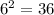`6^2=36` <-This is the square of the smaller.

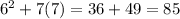`6^2+7(7)=36+49=85` <-This is the square of the smaller added to seven times the larger. We got 85 so the check is good.