Question

Determine whether the function below is an even function, an odd function, both, or neither.

f(x) = (x + 5)2
A. both even and odd
B. odd function
C. neither even nor odd
D. even function

Answer 1

A because like duhhhhhhhhh

Answer 2

neither even nor odd

Explanation:

f(x)=
`(x+5)^(2)`=
`x^(2) +10x+25`

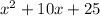
A function is an even function if f(-x) = f(x).

A function is an odd function if f(-x) = -f(x).

f(-x) =
`(-x+5)^(2)` =
`x^(2) -10x+25`

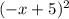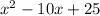
-f(x) =
`-x^(2) -10x-25`

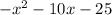
Clearly we can see that

f(-x) ≠ f(x)

f(-x) ≠ -f(x)

Hence the function is neither even nor odd.