Answer:
neither even nor odd
Explanation:
f(x)=
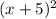 =
=
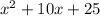
A function is an even function if f(-x) = f(x).
A function is an odd function if f(-x) = -f(x).
f(-x) =
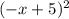 =
=
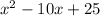
-f(x) =
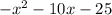
Clearly we can see that
f(-x) ≠ f(x)
f(-x) ≠ -f(x)
Hence the function is neither even nor odd.