Question

An electron (m=9.11x10^-31 kg) moves in a circle whose radius is 2.00x10^-2 m. If the force acting on the electron is 4.60x10^-14 N, what is it's speed?

Answer 1

The speed of the electron is
`3.178* 10^7\ m/s`.

Step-by-step explanation:

Given:

Mass of electron is,
`m=9.11* 10^(-31)\ kg`

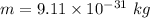
Radius of circle is,
`R=2.00* 10^(-2)\ m`

Force acting on the electron is,
`F=4.60* 10^(-14)\ N`

Now, we know that, for a circular turn, the force acting on the electron is due to centripetal force. Centripetal force acting on the electron is given as:

`F=(mv^2)/(R)`

Here, 'v' is the velocity of the electron.

Now, plug in all the given values and solve for 'v'. This gives,

`4.60* 10^(-14)=(9.11* 10^(-31)v^2)/(2.00* 10^(-2))\\\\9.11* 10^(-31)v^2=4.60* 10^(-14)* 2.00* 10^(-2)\\\\9.11* 10^(-31)v^2=9.2* 10^(-16)\\\\v^2=(9.2* 10^(-16))/(9.11* 10^(-31))\\\\v^2=1.01* 10^(15)\\\\v=\sqrt{1.01* 10^(15)}\\\\v=3.178* 10^7\ m/s`

Therefore, the speed of the electron is
`3.178* 10^7\ m/s`.