Answer:
The speed of the electron is
 .
.
Step-by-step explanation:
Given:
Mass of electron is,
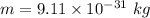
Radius of circle is,

Force acting on the electron is,

Now, we know that, for a circular turn, the force acting on the electron is due to centripetal force. Centripetal force acting on the electron is given as:

Here, 'v' is the velocity of the electron.
Now, plug in all the given values and solve for 'v'. This gives,

Therefore, the speed of the electron is
 .
.