Question

Do our emotions influence economic decisions? One way to examine the issue is to have subjects play an "ultimatum game" against other people and against a computer. Your partner get $10, on the condition that it be shared with you. The partner makes you an offer. If you refuse, neither of you gets anything. So it's to your advantage to accept even the unfair offer of $2 out of $10. Some people get upset and refuse even unfair offers. Here are data on the responses of 76 subjects randomly assigned to receive an offer of $2 from your partner:•Human offers had 20 accept and 18 reject, and•Computer offers had 32 accept and 6 rejectWe suspect that emotion will lead to offers from another person being rejected more often than offers from a computer. Determine the p-value for testing this conjecture.a. 0.3158b. 2.9613c. 0.0015d. 0.4737

Answer 1

C. 0.0015

Explanation:

Null hypothesis,

`H_0:P_H=P_c`

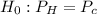
Alternative hypothesis,

`H_a:P_H>P_c`

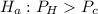
Sample proportions:

`P_H=(18)/(20+18)=0.473684\\\\P_c=(6)/(32+6)=0.157895`

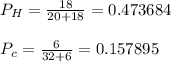
Pooled proportion,

`p=(x+y)/(n_1+n_2)=(18+6)/(76)=0.315789`

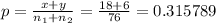
Under
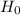`H_0`, the test statistic is given by,

`z_0=\frac{P_A-P_C}{\sqrt{P(1-P)((1)/(n_1)+(1)/(n_2))}}\\\\==\frac{0.473684-0.157895}{\sqrt{0.315789(1-0.315789)((1)/(38)+(1)/(38))}}=2.96`

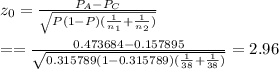
Since the alternative hypothesis is two tailed, the p-value is given by,

p-value= P(z > 2.96)=1 - P(Z ≤ 2.96)=1 - 0.9985

(FROM Z TABLE)

P-value = 0.0015