Answer:
C. 0.0015
Explanation:
Null hypothesis,
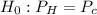
Alternative hypothesis,

Sample proportions:
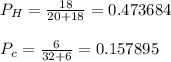
Pooled proportion,

Under
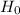 , the test statistic is given by,
, the test statistic is given by,
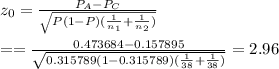
Since the alternative hypothesis is two tailed, the p-value is given by,
p-value= P(z > 2.96)=1 - P(Z ≤ 2.96)=1 - 0.9985
(FROM Z TABLE)
P-value = 0.0015