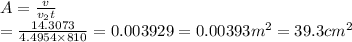Question

The water of a 14’ × 48’ metal frame pool can drain from the pool through an opening at the side of the pool. The opening is about h = 1.03 m below the water level. The capacity of the pool is V = 3780 gallons, the pool can be drained in t = 13.5 mins. P0 is the pressure of the atmosphere. rho is the density of the water.

(a) Write the Bernoulli's equation of the water at the top of the pool in terms of P_0, rho, h. Assuming the opening is the origin 0% deduction per feedback.
(b) Write the Bernoulli's equation of the water at the opening of the pool in terms of P_0, rho, h and v, where v is the speed at which the water leaves the opening. Assuming the opening is the origin.
(c) Express v^2 in terms of g and h.
(d) Calculate the numerical value of v in meters per second.
(e) Express the flow rate of the water in terms of V and t.
(f) Express the cross-sectional area of the opening, A, in terms of V, v and t.
(g) Calculate the numerical value of A in cm^2

Answer 1

Step-by-step explanation:

Height h = 1.03m

Volume v = 3780 gallons = 3780 * 0.0037851m^3 = 14.3073m^3

Time t = 13.5 mins = 13.5 * 60 = 810 seconds

Length of pool L = 14 inch = 14 * 2.54 = 35.56cm

width of pool b = 48 inch = 48 * 2.54 = 121.92 cm

a.) Consider the bernoulli's equation is given as:

`P_1+\rho gh_1 + (1)/(2)\rho v_1^2 = P_2 + \rho gh_2 + (1)/(2)\rho v_2^2 ...(1)`

consider the equation of bernoulli at the top of the pool

`P_0+\rho gh_1 + (1)/(2)\rho v_1^2 =constant ...(2)`

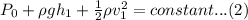
where
`P_1=P_0` atm pressure

At the top of the pool
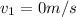`v_1=0m/s`, substitute in V_1 in equation (2)

`P_0+\rho gh_1 =constant ...(3)`

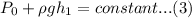
Hence equation (3) serves as the bernoullis equation at the top.

b.) Consider the equation of bernoulli's at the opening of the pool

`P_2+\rho gh_2 + (1)/(2)\rho v_2^2 =constant ...(4)\\P_0+\rho gh_2 + (1)/(2)\rho v_2^2 =constant ...(5)`

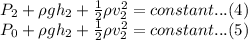
where
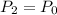`P_2=P_0` atm pressure and
`h_2=0m`

`P_0+\rho v_1^2 =constant ...(6)`

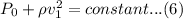
Hence equation (6) serves as the bernoullis equation of water at the opening of the pool.

c.) Consider the equation (3) and (4)

`P_0+\rho gh_1 =P_0+\rho v_1^2\\\\(1)/(2)\rho v_2^2=\rho gh_1\\v_2^2=2gh_1\\v_2=(√(2gh_1))m/s...(7)`

Hence velocity is
`v_2=(√(2gh_1))m/s`

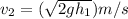
d.) consider (7)

`v_2=(√(2(9.81)(1.03)))=4.4954m/s(approx)`

This is the norminal value of velocity

e.) consider the equation of flow rate interval of v and t

flow(t)=
`(dv)/(dt)(m^3/s)` hence this is the flow rate

f.) Consider the equation cross sectional area in terms of V,v2 and t

`AV_2=(v)/(t)\\\\A=(v)/(v_2t)(m^2)...8`

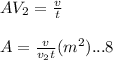
hence this serves as the cross sectional area.

g.) Consider the equation of area from equation (8)

`A=(v)/(v_2t)\\=(14.3073)/(4.4954* 810)=0.003929=0.00393m^2=39.3cm^2`