Question

Air contained in a rigid, insulated cubic tank of edge 1 m, fitted with a paddle wheel, undergoes a stirring process between State 1: T1 = 40 °C, P1 = 400 kPa; and State 2: P2 = 800 kPa.

(a). (4p) Please determine the temperature change in this process.
(b). (4p) Please determine the work done by the paddle wheel in this stirring process.
(c). (4p) Please determine the entropy generation in this process.

Answer 1

Step-by-step explanation:

Given that the tank is insulated and rigid, heat transfer to the surrounding is zero and there is no change in volume of system(container).

p1=400kpa, T1= 40°c= 313k, p2=800kpa

volume of container = volume of cube= a³=1³=1m³

Air is acting as an ideal gas, hence, applying ideal gas equatin
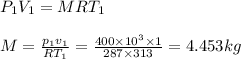`P_1V_1=MRT_1\\\\M=(p_1v_1)/(RT_1)=(400* 10^3 * 1)/(287* 313)=4.453kg` R= 287J/kg.k for air

a.) Process 1-2 constant volume process v1=v2

P∝T=
`(P_1)/(P_2)=(T_1)/(T_2)=(400)/(800)=(313)/(T_2)\\\\T_2=626K =353^oC`

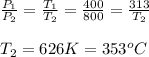
b.) According to first law of thermodynamics

`\deltaQ=dv+d\omega`

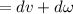
δQ=0(insulated container)

`0=dv+d\omega\\d\omega=-dv=-mc_v\delta T`

`c_v=(1)/(r-1)R`

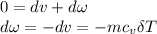
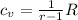
where r= specific heat ratio; for air, r=1.4, R= 0.287KJ/kg.k

`c_v=(1)/(r-1)R=(1)/(1.4-1)0.287=0.7175KJ/kg.k`

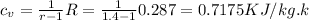
Then

`d\omega=-dv=-mc_v\delta T=-4.453* 0.7175\tims (626-313)=-1000.043KJ`

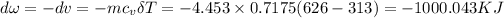
The negative sign means work done of system is in reverse.

c.) Entropy generation = change in system + change in surrounding

change in surrounding is zero

change in system=
`mc_vln((T_2)/(T_1))+ mrln((v_2)/(v_1))`

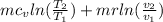
v1=v2; v2/v1=1; ln(1)=0

entropy gen= 4.453*0.7175*ln(626/313) + 0 =2.215KJ/k