Question

Abby, Billy and Cathy fire one shot each at a target. The probability that Abby will hit the target is 1/5. The probability that Billy will hit the target is 1/4. The probability that Cathy will hit the target is 1/3.

If they fire together, calculate the probability that:

1. All three shots hit the target

2. Only Cathy's shot hits the target

3. At least one shot hits the target

Answer 1

1. 0.0167

2. 0.2

3. 0.6

Explanation:

Probabilities on Independent Events

If A and B are independent events (the occurrence of A doesn't affect the occurrence of B and vice-versa), then the probability that both events occur is

`\displaystyle P(A\bigcap B)= \ P(A).P(B)`

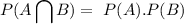
Being P(A) and P(B) the individual probability of each independent event

The probability that A does not occur is

`\displaystyle P(\bar{A})=1-P(A)`

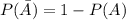
The probability that B does not occur is

`\displaystyle P(\bar{B})=1-P(B)`

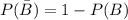
The probability that C does not occur is

`\displaystyle P(\bar{C})=1-P(C)`

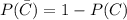
We have 3 independent events. We know that because they fire together, no mutual affectation can happen

.

The probability that Abby will hit the target is 1/5.

`\displaystyle P(A)=(1)/(5)`

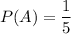
The probability that Billy will hit the target is 1/4.

`\displaystyle P(B)=(1)/(4)`

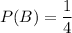
The probability that Cathy will hit the target is 1/3

`\displaystyle P(C)=(1)/(3)`

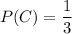
Part 1.

The probability that all three shots hit the target is

`\displaystyle P(A\bigcap B\bigcap C)=(1)/(5).(1)/(4).(1)/(3)`

`\displaystyle P(A\bigcap B\bigcap C)=(1)/(60)`

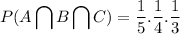
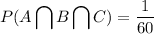
The probability that all three shots hit the target is

`\displaystyle P= (1)/(60)=0.0167`

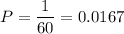
Part 2.

The probability that only Cathy's shot hits the target is computed assuming Abby and Billy won't succeed

.

`\displaystyle P(\bar{A}\bigcap \bar{B}\bigcap C)=P(\bar{A})\  P(\bar{B})\ P(C)=(1-(1)/(5))\ (1-(1)/(4))\ ((1)/(3))=(4)/(5).(3)/(4).(1)/(3)=(1)/(5)=0.2`

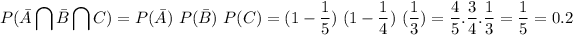
3.

The probability that at least one shot hits the target is when one of them succeeds, two of them succed or all of them succeed

`\displaystyle P(A\bigcap \bar{B}\bigcap \bar{C})+P(\bar{A}\bigcap {B}\bigcap \bar{C})+P(\bar{A}\bigcap\bar{B}\bigcap C)+P(A\bigcap B\bigcap \bar{C})+P(A\bigcap \bar{B}\bigcap C)+P(\bar{A}\bigcap B\bigcap C)+P(A\bigcap B\bigcap C)`

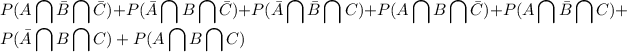
But it's easier to find the negated probability of the above, i.e. we compute the probability that NO ONE hits the target and subtract it from 1

`\displaystyle P=1-P(\bar{A}\bigcap \bar{B}\bigcap \bar{C})`

`P=1 -(1-(1)/(5))(1-(1)/(4))(1-(1)/(3))=1-(4)/(5).(3)/(4).(2)/(3)=1-(2)/(5)=(3)/(5)`

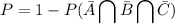
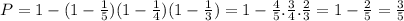
P=0.6