Answer:
1. 0.0167
2. 0.2
3. 0.6
Explanation:
Probabilities on Independent Events
If A and B are independent events (the occurrence of A doesn't affect the occurrence of B and vice-versa), then the probability that both events occur is
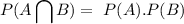
Being P(A) and P(B) the individual probability of each independent event
The probability that A does not occur is
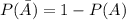
The probability that B does not occur is
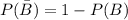
The probability that C does not occur is
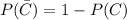
We have 3 independent events. We know that because they fire together, no mutual affectation can happen
.
The probability that Abby will hit the target is 1/5.
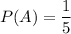
The probability that Billy will hit the target is 1/4.
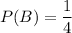
The probability that Cathy will hit the target is 1/3
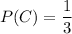
Part 1.
The probability that all three shots hit the target is

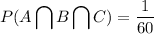
The probability that all three shots hit the target is
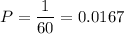
Part 2.
The probability that only Cathy's shot hits the target is computed assuming Abby and Billy won't succeed
.

3.
The probability that at least one shot hits the target is when one of them succeeds, two of them succed or all of them succeed
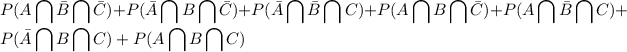
But it's easier to find the negated probability of the above, i.e. we compute the probability that NO ONE hits the target and subtract it from 1
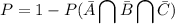
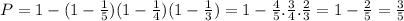
P=0.6