Answer:
The basis is <1/√3, -2/5 x + 1 /15, 0.4825x^2 - 0.6466 x -0.3748>
Explanation:
First, we calculate the norm of f
||f||² = <f,f> = f(-1)²+f(0)²+f(1)² ) = 3*(-7)² = 147
Therefore, ||f|| = √147
We take as the first element of the basis

we define
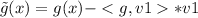
lets calculate <g,v1>
g(-1) = 9
g(0) = 5
g(1) = 1
v1(-1) = v1(0) = v1(1) = 1/√3
Then <g,v1> = 9*7/√(147)+5*7/√(147)+1*7/√(147) = 15*7/√(147) = 105/√147
and <g,v1>v1 = 105/√(147) * 7/√(147) = 735/147 = 35/9
Therefore,
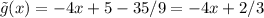
Now, lets calculate the norm, for that
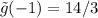
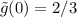
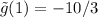
As a result,
![< \tilde{g}, \tilde{g} > = (14/3)^2+(2/3)^2+(-10/3)^2 = 100, hence [tex] || \tilde{g} || = 10](https://img.qammunity.org/2020/formulas/mathematics/high-school/lulcf8v3vhjovvga9s12u67n0wkzzgve3f.png)
We take
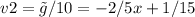
Finally, we take
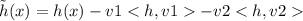
Note that
h(-1) = 7
h(0) = -5
h(1) = -9
v1(-1) = v1(0) = v1(1) = 7/√(147) = 1/√3
v2(-1) = 7/15
v2(0) = 1/15
v3(1) = -1/3
Thus,
<h,v1>v1 = (7-5-9)*(7/√(147))² = -7/3
<h,v2>v2 = ((7*7/15) + (-5*1/15) + (-9*-1/3)) * (-2/5 x + 1 /15) = -66/25 x + 11/25
As a consecuence, we have that

since
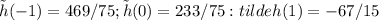
we obtain that

Therefore,
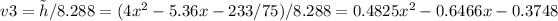
The basis is <1/√3, -2/5 x + 1 /15, 0.4825x^2 - 0.6466 x -0.3748>