Question

A random sample of 66 bags of white cheddar popcorn​ weighed, on​ average, 5.43 ounces with a standard deviation of 0.25 ounce.

Test the hypothesis that μ = 5.7 ounces against the alternative​ hypothesis, μ < 5.7 ​ounces, at the 0.05 level of significance.

Answer 1

Answer with explanation:

As per given , we have to test hypothesis :

`H_0:\mu=5.7\\\\ H_a:\mu<0.57` , where
`\mu` = Population mean.

Since the alternative hypothesis is left--tailed , so test is a left-tailed test.

Sample size : n=66

Sample mean :
`\overline{x}=5.43`

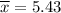
sample standard deviation : s= 0.25

Also, population standard deviation is not given , so we will perform a left tailed t-test.

Test statistics :
`t=\frac{\overline{x}-\mu}{(s)/(√(n))}`

`t=(5.43-5.7)/((0.25)/(√(66)))`

`t=(-0.27)/((0.25)/(8.12403840464))\approx-8.77`

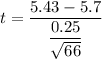
For significance level 0.05 and degree of freedom 65 (df=n-1), we have

Critical t-value =
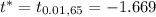`t^*=t_(0.01, 65)=-1.669` [Using student's t-distribution table]

Decision : Since -8.77(calculated t- value)< -1.669(Critical value) , it means it falls under rejection region.

i.e. We reject the null hypothesis.

Conclusion : We have sufficient evidence to support the alternative hypothesis μ < 5.7 ​ounces .