Answer with explanation:
As per given , we have to test hypothesis :
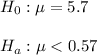 , where
, where
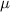 = Population mean.
= Population mean.
Since the alternative hypothesis is left--tailed , so test is a left-tailed test.
Sample size : n=66
Sample mean :
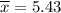
sample standard deviation : s= 0.25
Also, population standard deviation is not given , so we will perform a left tailed t-test.
Test statistics :
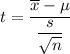
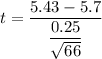

For significance level 0.05 and degree of freedom 65 (df=n-1), we have
Critical t-value =
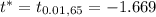 [Using student's t-distribution table]
[Using student's t-distribution table]
Decision : Since -8.77(calculated t- value)< -1.669(Critical value) , it means it falls under rejection region.
i.e. We reject the null hypothesis.
Conclusion : We have sufficient evidence to support the alternative hypothesis μ < 5.7 ounces .