Question

A 2.5 kg box has an initial velocity of 3.9 m/s upward along a plane inclined at 23◦ to the horizontal. The coefficient of kinetic friction between the box and the plane is 0.27. The acceleration of gravity is 9.81 m/s 2 . How far up the incline does the box travel? Answer in units of m.

Answer 1

The box will travel 1.2 [m]

Step-by-step explanation:

This problem can easily be solved by using the principle of work and energy conservation which expresses that, when the particle moves from A1 to A2 under the action of an F force, the work of the F Force is equal to the change of the kinetic energy of the particle. The above is known as the principle of work and energy.

In the attached image we can see the conditions of this particular case, and we will analize each member of the equations deducted:

Kinetic energy (position 1):

`E_(k1)=(1)/(2)*m*v_(0)^(2) \\E_(k1)=(1)/(2) *2.5*(3.9)^(2) \\E_(k1)=19 [J]`

Position 2 (work):

`W= - f_(fri)*x - (m*g*sin(23))*x\\W= - f_(fri)*x - (2.5*9.81*sin(23))*x\\\\W= - (f_(fri)* +9.5)*x\\`

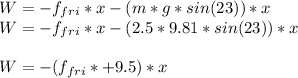
Principle of work and energy:

`Ek_(1) +W=Ek_(2) \\Ek_(1) +W=0 \\\\Ek_(1) =-W \\`

`19=(f_(fri) +9.5 )*x`

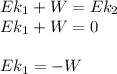
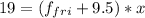
In the last equation we need to clear x, but first we need to find the value for the friction force, Therefore in the attached image we can find the study of forces in the y axis where we cand find the normal force, then knowing the friction factor we will determine the friction force.

`x=(19)/((f_(fri)+9.5 )) \\x=(19)/((6.09+9.5 )) \\\\x=1.21[m]`