Answer:
Therefore, height of the wall at which the ladder is placed is AB = 39.12 foot.
Explanation:
Let,
AB = height of the wall at which the ladder is placed
AC = height of the ladder = 40 foot
BC = distance from the wall to the base of the ladder = 8 feet
To Find:
AB = height of the wall at which the ladder is placed = ?
Solution:
Consider a right angled triangle Δ ABC right angle at angle B,
So by Pythagoras theorem we have
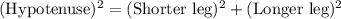
AC² = AB² + BC²
Substituting the given values in above equation we get
40² = AB² + 8²
∴ AB² = 40² - 8²
∴ AB² = 1536
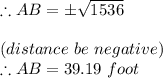
Therefore, height of the wall at which the ladder is placed is AB = 39.12 foot.