Answer:
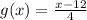
Explanation:
Alright, lets get started.
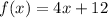
Suppose y is f(x), then
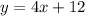
For finding inverse function, lets interchange the variables x and y
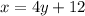
Subtracting 12 form both sides
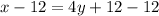
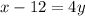
Dividing 4 in both sides
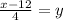
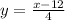
Hence the inverse of f(x) is
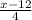
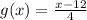 ..................Answer
..................Answer
Hope it will help :)