Question

Determine the equivalent system for the given system of equations.

4x − 5y = 2
3x − y = 8

4x − 5y = 2
13x − 8y = 4
4x − 5y = 2
10x + 3y = 15
4x − 5y = 2
13x − 8y = 26
4x − 5y = 2
7x + 6y = 10

Answer 1

The answer is

(4x - 5y = 2) and (13x - 8y =26)

Answer 2

4x − 5y = 2

13x − 8y = 26

Explanation:

The equivalent system must have the same solution as the given system of equations:

4x − 5y = 2

3x − y = 8

Here we have that:

y = 3x - 8

4x - 5y = 2

4x - 5(3x - 8) = 2

4x - 15x + 40 = 2

-11x = -38

`x = (38)/(11)`

`y = 3x - 8 = (3*38)/(11) - (88)/(11) = (26)/(11)`

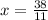
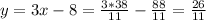
Now, we have to verify which of these systems have this answer:

4x − 5y = 2

13x − 8y = 4

13x - 8y = 4

`13(38)/(11) - 8(26)/(11) = (286)/(11) \\eq 4`

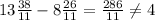
4x − 5y = 2

10x + 3y = 15

10x + 3y = 15

`10(38)/(11) + 3(26)/(11) = (458)/(11) \\eq 15`

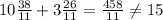
4x − 5y = 2

13x − 8y = 26

4x - 5y = 2

`4(38)/(11) - 5(26)/(11) = (22)/(11) = 2`

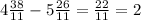
13x - 8y = 26

`13(38)/(11) - 8(26)/(11) = (286)/(11) = 26`

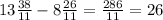
This is the correct answer

So this is the correct answer

4x − 5y = 2

7x + 6y = 10