Step-by-step explanation:
Conversion of a quadratic equation from standard form to vertex form is done by completing the square method.
Assume the quadratic equation to be
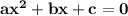 where x is the variable.
where x is the variable.
Completing the square method is as follows:
- send the constant term to other side of equal
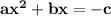
- divide the whole equation be coefficient of
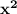 , this will give
, this will give
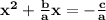
- add
 to both side of equality
to both side of equality
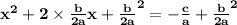
- Make one fraction on the right side and compress the expression on the left side

- rearrange the terms will give the vertex form of standard quadratic equation

Follow the above procedure will give the vertex form.
(NOTE : you must know that
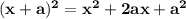 . Use this equation in transforming the equation from step 3 to step 4)
. Use this equation in transforming the equation from step 3 to step 4)