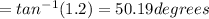Question

PLEASE NEED THIS DONE AS FAST AS POSSIBLE!!!!!!!!!!!!!!!!!
IT MUST BE CORRECT

Answer 1

1)7.288 feet

2)11.6 feet

3)safe

4) 3.7 feet

5) ∅
`= tan^(-1)(1.5) = 56.31 degrees`

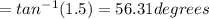
6)∅1
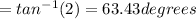
`= tan^(-1)(2) = 63.43 degrees`

∅2
`= tan^(-1)(1.2) = 50.19 degrees`

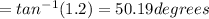
Explanation:

1) The door barn is rectangular in shape. The length is 9 feet and The angle between diagonal and side is 39 degrees.

Applying trigonometry,

tan(39) =
`(opposite)/(adjacent) = (s)/(9)` = 0.809

Thus, s=
`(9)(0.809) = 7.288 feet`

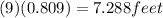
2) Applying pythagoras theorm,

`(Diagonal)^(2) = (9)^(2) + (7.288)^(2) =134.115`

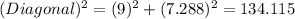
Diagonal length (d) = 11.58 feet. Nearest tenth place = 11.6 feet

3) The length of ladder is 14 foot and height from ground is 13.5 feet.

Applying trigonometry,

sin(∅) =
`(opposite)/(hypotenous) = (13.5)/(14)` = 0.964

∅ = angle of elevation =
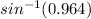`sin^(-1)(0.964)` = 74.57 ≈ 75 degrees.

Thus tractor can climb safely.

4)Applying, pythgoras theorm,

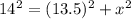
`14^(2) = (13.5)^(2)  + x^(2)`

x =
`\sqrt{14^(2)-(13.5)^(2)} = 3.708`

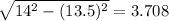
Thus, ladder should be placed at distance 3.7 feet

5)Let angle of elevation be ∅.

tan(∅) =
`(30)/(20) = 1.5`

∅
`= tan^(-1)(1.5) = 56.31 degrees`

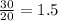
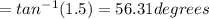
6)After moving 5 feet closer to barn, Let angle of elevation for light near barn be ∅1 and for farther one be ∅2.

Thus,

tan(∅1) =
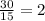
`(30)/(15) = 2`

∅1
`= tan^(-1)(2) = 63.43 degrees`

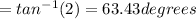
tan(∅2) =
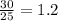
`(30)/(25) = 1.2`

∅2
`= tan^(-1)(1.2) = 50.19 degrees`