Question

6A certain load and set of slings create a 20-degree angle between the load and each sling leg. Using a spreader for the same lift would result in a 60-degree angle between the load and each sling leg. What is the reduction (in percent) in sling stress and in the horizontal reaction when the spreader is used?

Answer 1

The angle between the sling and the load is
`20^(\circ)`

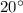
So the tension in each sling can be calculated as

`Sin \theta = Mg => T = (Mg)/(2Sin\theta)`

`Sin \theta=> (Mg)/(2Sin 20^(\circ))`

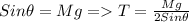
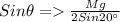
Where

M is the mass of the load

The Horizontal reaction on the sling will be inward.

After using the spreader, the new angle between sling and load is
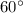`60^(\circ)`, the tension in the sling will be

`T= (Mg)/(2 Sin 60^(\circ))` =
`(Mg)/(2 Sin 20^(\circ))`

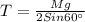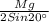
The tension will be same as before in the sling move away through the spreader at an angle more than 90 degree the horizontal force will act opposite and will be outward