Solution:
The angle between the sling and the load is
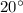
So the tension in each sling can be calculated as
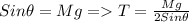

Where
M is the mass of the load
The Horizontal reaction on the sling will be inward.
After using the spreader, the new angle between sling and load is
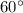 , the tension in the sling will be
, the tension in the sling will be
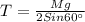 =
=
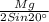
The tension will be same as before in the sling move away through the spreader at an angle more than 90 degree the horizontal force will act opposite and will be outward