Question

An astronaut shipwrecked on a distant planet with unknown characteristics is on top of a cliff, which she wishes to descend. She does not know the acceleration due to gravity on the planet, and she has only a good watch with which to make measurements. She wants to learn the height of the cliff, and to do this she makes two measurements. She wants to learn the height of the cliff, and to do this she makes two measurements. First, she lets the rock fall from rest off the cliff edge; she finds that the rock takes 4.15sec to reach the distant ground below the cliff. Second, she releases the rock from the same spot but tosses it upward so that it rises 2 m before falling to the distant ground below the cliff. This time the rock takes 6.30 s to reach the ground. What is the height of the cliff?

Answer 1

y = 9.64 m

Step-by-step explanation:

This exercise should be solved using kinematics in one dimension, let's write the equations for the two cases presented

The rock is released

y = y₀ + V₀₁ t₁ - ½ g t₁²

In this case the speed starts is zero

y = y₀ - ½ g t₁²

The rock ​​is thrown up

y = y₀ + v₀² t₂ -½ g t₂²

The height that reaches the floor is zero

y₀ - ½ g t₁² = y₀ + v₀₂ t₂ - ½ g t₂²

We use the initial velocity with the equation

v₂² = v₀₂² - 2 g y

At the point of maximum height v₂ = 0

v₀₂ = √ (2 g
`y_(max)`)

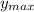g (-t₁² + t₂²) = 2 √ (2 g
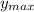`y_(max)`) t₂²

g (- 4.15² + 6.30²) = 2 √ (2 2 g) 6.3

g (22.4675) = 25.2 √ g

g² = 2²5.2 / 22.4675 g

g = 1.12 m / s²

Having the value of g we can use any equation to find the height

y = ½ g t₁²

y = ½ 1.12 4.15²

y = 9.64 m