Answer:
The wavelength of the light is 446.8 nm.
Step-by-step explanation:
Given that,
Width = 0.705 mm
Distance = 2.13 m
Diffraction pattern = 1.35 mm
Number of order = 1
We need to calculate the wavelength of light
Using formula of wavelength


Put the value into the formula
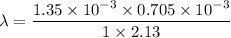
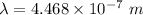
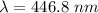
Hence, The wavelength of the light is 446.8 nm.