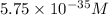Question

Calculate the ratio of [Cu2+]/[Cu+] in an aqueous solution at Eh = + 0.80 volt.​

Answer 1

Answer: The ratio of
`[Cu^(2+)]/[Cu^+]` in an aqueous solution is
`5.75* 10^(-35)M`

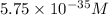
Step-by-step explanation:

The substance having highest positive
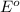`E^o` potential will always get reduced and will undergo reduction react.

Oxidation half reaction:
`Cu(s)\rightarrow Cu^(2+)(aq.)+2e^-;E^o_(Cu^(2+)/Cu)=+0.34V`

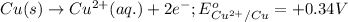
Reduction half reaction:
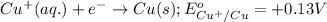`Cu^+(aq.)+e^-\rightarrow Cu(s);E^o_(Cu^+/Cu)=+0.13V` ( × 2)

Net cell reaction:
`2Cu^+(aq.)\rightarrow Cu^(2+)(aq.)+Cu(s)`

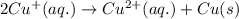
Substance getting oxidized always act as anode and the one getting reduced always act as cathode.

To calculate the
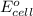`E^o_(cell)` of the reaction, we use the equation:

`E^o_(cell)=E^o_(cathode)-E^o_(anode)`

`E^o_(cell)=0.13-(0.34)=-0.21V`

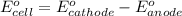
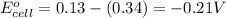
To calculate the EMF of the cell, we use the Nernst equation, which is:

`E_(cell)=E^o_(cell)-(0.059)/(n)\log ([Cu^(2+)])/([Cu^(+)]^2)`

Concentration of pure solids and liquids are taken as 1 in the ratio

where,

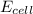`E_(cell)` = electrode potential of the cell = +0.80 V

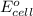`E^o_(cell)` = standard electrode potential of the cell = -0.21 V

n = number of electrons exchanged = 2

`([Cu^(2+)])/([Cu^+]^2)` = Ratio of the concentration

Putting values in above equation, we get:

`0.80=-0.21-(0.059)/(2)* \log(([Cu^(2+)])/([Cu^(+)]^2))\\\\([Cu^(2+)])/([Cu^(+)]^2)=5.75* 10^(-35)M`

Hence, the ratio of
`[Cu^(2+)]/[Cu^+]` in an aqueous solution is
`5.75* 10^(-35)M`