Question

Please help Need good grade

A placekicker kicks a football upward at an angle of 60 and a speed of 5.0 m/s at what other angle will he have to kick a second ball with the same speed to reach the same distance downrange ignore air resistance

45

30

15

90

Answer 1

30 degrees

Step-by-step explanation:

Answer 2

The other angle is 120°.

Step-by-step explanation:

Given that,

Angle = 60

Speed = 5.0

We need to calculate the range

Using formula of range

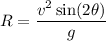`R=(v^2\sin(2\theta))/(g)`...(I)

The range for the other angle is

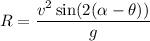`R=(v^2\sin(2(\alpha-\theta)))/(g)`....(II)

Here, distance and speed are same

On comparing both range

`(v^2\sin(2\theta))/(g)=(v^2\sin(2(\alpha-\theta)))/(g)`

`\sin(2\theta)=\sin(2*(\alpha-\theta))`

`\sin120=\sin2(\alpha-60)`

`120=2\alpha-120`

`\alpha=(120+120)/(2)`

`\alpha=120^(\circ)`

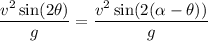
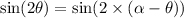
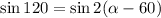
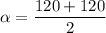
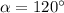
Hence, The other angle is 120°