Answer:
The other angle is 120°.
Step-by-step explanation:
Given that,
Angle = 60
Speed = 5.0
We need to calculate the range
Using formula of range
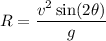 ...(I)
...(I)
The range for the other angle is
 ....(II)
....(II)
Here, distance and speed are same
On comparing both range
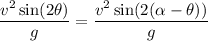
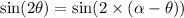
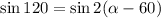
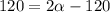
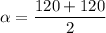
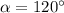
Hence, The other angle is 120°