Question

AB = x + 2

DC = 22 − x
AD = 6 + y
BC = 3y
Quadrilateral ABCD is a parallelogram if both pairs of opposite sides are congruent. Show that quadrilateral ABCD is a parallelogram by finding the lengths of the opposite side pairs.
A) 6, 3
B) 9, 6
C) 12, 6
D) 12, 9

Answer 1

D

Explanation:

Answer 2

Option D) 12, 9

Explanation:

we know that

In a parallelogram opposite side are parallel and congruent

so

In the parallelogram ABCD

opposite sides are

AB and DC

BC and AD

so

AB=CD

BC=AD

step 1

Find the value of x

AB=DC

substitute the values

`x+2=22-x`

solve for x

`x+x=22-2`

`2x=20`

`x=10`

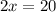
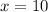
step 2

Find the value of side AB

`AB=x+2`

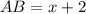
substitute the value of x

`AB=10+2=12\ units`

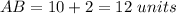
step 3

Find the value of y

BC=AD

substitute the values

`3y=6+y`

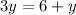
solve for y

`3y-y=6`

`2y=6`

`y=3`

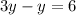
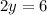
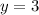
step 4

Find the value of BC

`BC=3y`

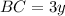
substitute the value of y

`BC=3(3)=9\ units`

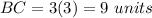
therefore

The length of the opposite side pairs are 12 and 9