Answer:
Option D) 12, 9
Explanation:
we know that
In a parallelogram opposite side are parallel and congruent
so
In the parallelogram ABCD
opposite sides are
AB and DC
BC and AD
so
AB=CD
BC=AD
step 1
Find the value of x
AB=DC
substitute the values
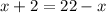
solve for x

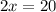
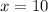
step 2
Find the value of side AB
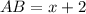
substitute the value of x
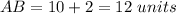
step 3
Find the value of y
BC=AD
substitute the values
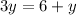
solve for y
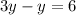
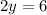
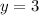
step 4
Find the value of BC
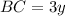
substitute the value of y
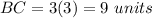
therefore
The length of the opposite side pairs are 12 and 9