Answer:
a)
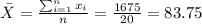

b) The 90% confidence interval would be given by (72.551;94.949)
c)We are 90% confident that the true mean temperature for the sleeping bags it's between 72.551 and 94.949
Explanation:
Data set given
80,90,100,120,75,37,30,23,100,110 105,95,105,60,110,120,95,90,60,70
Part a
We can calculate the sample mean and the sample deviation with the following formulas:
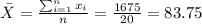

Part b
The confidence interval for the mean is given by the following formula:
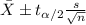 (1)
(1)
In order to calculate the critical value
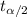 we need to find first the degrees of freedom, given by:
we need to find first the degrees of freedom, given by:
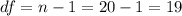
Since the Confidence is 0.90 or 90%, the value of
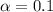 and
and
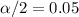 , and we can use excel, a calculator or a table to find the critical value. The excel command would be: "=-T.INV(0.05,19)".And we see that
, and we can use excel, a calculator or a table to find the critical value. The excel command would be: "=-T.INV(0.05,19)".And we see that

Now we have everything in order to replace into formula (1):
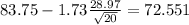
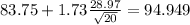
So on this case the 90% confidence interval would be given by (72.551;94.949)
Part c
We are 90% confident that the true mean temperature for the sleeping bags it's between 72.551 and 94.949