Answer:
Option D.
Explanation:
The given expression is

Here, n=9, p=x^2 adn q=-x.
kth term in the binomial expansion of
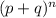 is
is
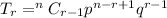
First term of the binomial expansion of
 is
is
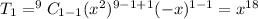
Second term of the binomial expansion of
 is
is
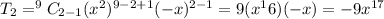
Third term of the binomial expansion of
 is
is
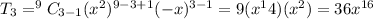
Last or 10th term of the binomial expansion of
 is
is
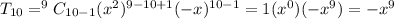
Therefore, the correct option is D.