Question

Evaluate the function g(x)-2x^2+3x-5 fpr the input values -2,0,and 3

Answer 1

g(-2) = -3, g(0) = -5 and g(3) = 22

Explanation:

Here, the given function is:
`g(x) = 2x^2 + 3 x - 5`

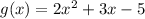
Now, evalutaing the function at x = -2, 0 and 3

Substituting x = -2 in g(x):

`g(-2) = 2(-2)^2 + 3 (-2) - 5  = 2(4) - 6 - 5 = 8 -11  = -3\\\implies g(-2)  = -3`

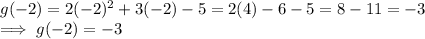
Substituting x = 0 in g(x):

`g(0) = 2(0)^2 + 3 (0) - 5  = 0 + 0 - 5 = -5\\\implies g(0)  = -5`

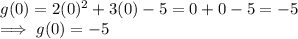
Substituting x = 3 in g(x):

`g(3) = 2(3)^2 + 3 (3) - 5  = 2(9) + 9 - 5 = 18 + 9- 5 = 27 -5  = 22\\\implies g(3)  =22`

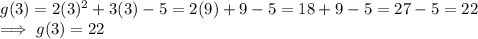
Hence, g(-2) = -3, g(0) = -5 and g(3) = 22.