Answer: (1.375, 18.625 )
Explanation:
The confidence interval for population mean is given by :-
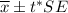 (1)
(1)
, where
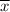 = sample mean
= sample mean
t* = critical value.
SE = standard error
As per given , we have
n= 21
Degree of freedom : df = n-1=21-1=20
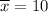
Significance level :
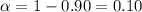
Standard error : SE= 5
The critical t-value for confidence interval is a two-tailed value with respect to the given degree of freedom i.e.
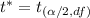 .
.
Using student's t-distribution table ,
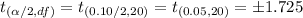
The 90% confidence interval will be :
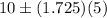 [by formula in (1)]
[by formula in (1)]
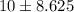
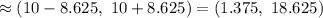
Hence, the limits of the confidence interval=(1.375, 18.625 )