Question

Find the limit of the function algebraically. (2 points) limit as x approaches zero of quantity x squared plus two x divided by x to the fourth power.

Answer 1

DNE

Explanation:

`\lim_(x \to \0) (x^(2) +2x)/(x^(4) )`

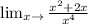
As you can see in the picture I attached to this, that as the limit goes to zero from the negative side, it approaches -∞ and from the positive side, it approaches ∞ . hence, the limit doesn't exist.

To show this algebraically, you have to imagine how a number divided by zero looks like, Just know the graph of 1/x and see how the limit to zero doesnot exist. I hope this helps!