Answer:
7.67001846 km/s or 17157.38529 mph
Step-by-step explanation:
G = Gravitational constant = 6.67 × 10⁻¹¹ m³/kgs²
M = Mass of the Earth = 5.972 × 10²⁴ kg
m = Mass of satellite
v = Velocity of satellite
The distance between the Earth's center and the satellite is
r = 6371000+400000 = 6771000 m
As the centripetal force balances the force of gravity we have
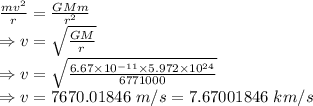
Converting to mph
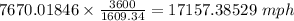
The velocity of the satellite is 7.67001846 km/s or 17157.38529 mph