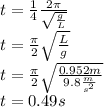Question

A simple pendulum is made from a 0.952-m-long string and a small ball attached to its free end. The ball is pulled to one side through a small angle and then released from rest. After the ball is released, how much time elapses before it attains its greatest speed?

Answer 1

It would take 45 seconds

Step-by-step explanation:

Answer 2

`t=0.49s`

Step-by-step explanation:

The ball reaches its greatest speed at the lowest point, since at this point its gravitational potential energy is zero, therefore its kinetic energy is maximum. The time at which it reaches its lowest point is:

`t=(T)/(4)`

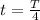
Here T is the pendulum period:

`T=(2\pi)/(\omega)`

Here
`\omega` is the natural frequency of the system:

`\omega=\sqrt{(g)/(L)}`

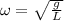
Replacing this values:

`t= (1)/(4)\frac{2\pi}{\sqrt{(g)/(L)}}\\t=(\pi)/(2)\sqrt{(L)/(g)}\\t=(\pi)/(2)\sqrt{(0.952m)/(9.8(m)/(s^2))}\\t=0.49s`