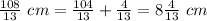Question

A rectangle has a length of (x + 4) centimeters and a width of 12x centimeters. If the perimeter is 26 centimeters, what is the width of the rectangle.

Answer 1

Explanation:

Answer 2

The width of rectangle is
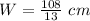`W=(108)/(13)\ cm` or
`8(4)/(13)\ cm`

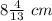
Explanation:

we know that

The perimeter of rectangle is equal to

`P=2(L+W)`

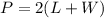
where

L is the length of rectangle

W is the width of rectangle

we have

`P=26\ cm\\L=(x+4)\ cm\\W=12x\ cm`

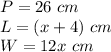
substitute

`26=2(x+4+12x)`

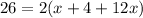
solve for x

`26=2(13x+4)`

`26=26x+8`

`26x=26-8`

`26x=18`

`x=(18)/(26)`

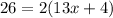
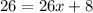
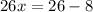
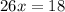
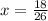
simplify

`x=(9)/(13)`

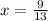
Find the width of rectangle

`W=12x\ cm`

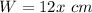
substitute the value of x

`W=12((9)/(13))=(108)/(13)\ cm`

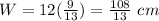
Convert to mixed number

`(108)/(13)\ cm=(104)/(13)+(4)/(13)=8(4)/(13)\ cm`