Answer with explanation:
Given : A standardized exam's scores are normally distributed. In a recent year, the mean test score was 1530 and the standard deviation was 316.
i.e.
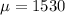 and
and
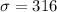 .
.
Usual values have a z-score between -1.96 and 1.96.
The test scores of four students selected at random are 1930, 1250, 2250, and 1420.
Formula for z :
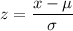
For x= 1930 ,
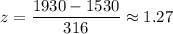
The z-score for 1930 is 1.27.
For x= 1250 ,
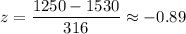
The z-score for 1250 is -0.89.
For x=2250 ,
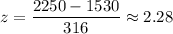
The z-score for 1250 is 2.28 .
For x= 1420 ,
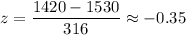
The z-score for 1250 is -0.35 .
Since all the z-values lie between -1.96 and 1.96 except 2.28 corresponding to x=2250.
Thus , the z-score corresponding to x=2250 is unusual.