Question

A standardized exam's scores are normally distributed. In a recent year, the mean test score was 1530 and the standard deviation was 316. The test scores of four students selected at random are 1930. 1250. 2250. and 1420. Find the z-scores that correspond to each value and determine whether any of the values are unusual. The z-score for 1930 is.(Round to two decimal places as needed.)

Answer 1

Answer with explanation:

Given : A standardized exam's scores are normally distributed. In a recent year, the mean test score was 1530 and the standard deviation was 316.

i.e.
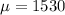`\mu=1530` and
`\sigma=316` .

Usual values have a z-score between -1.96 and 1.96.

The test scores of four students selected at random are 1930, 1250, 2250, and 1420.

Formula for z :
`z=(x-\mu)/(\sigma)`

For x= 1930 ,
`z=(1930-1530)/(316)\approx1.27`

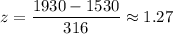
The z-score for 1930 is 1.27.

For x= 1250 ,
`z=(1250-1530)/(316)\approx-0.89`

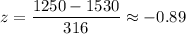
The z-score for 1250 is -0.89.

For x=2250 ,
`z=(2250-1530)/(316)\approx2.28`

The z-score for 1250 is 2.28 .

For x= 1420 ,
`z=(1420-1530)/(316)\approx-0.35`

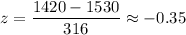
The z-score for 1250 is -0.35 .

Since all the z-values lie between -1.96 and 1.96 except 2.28 corresponding to x=2250.

Thus , the z-score corresponding to x=2250 is unusual.