A recent survey of 50 executives who were laid off during a recent recession revealed it took a mean of 26 weeks for them to find another position. The standard deviation of the…

Question

asked Apr 16, 2020 192k views

1 Answer

Jlarsch · Answer 1 · 2020-04-22T03:45:44+0000

Formula to find the confidence interval for population mean :-

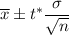
$\overline{x}\pm t^*(\sigma)/(√(n))$

, where
$\overline{x}$ = sample mean.

t*= critical z-value

n= sample size.

s= sample standard deviation.

By considering the given question , we have

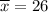
$\overline{x}= 26$

s=6.2

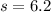
n= 50

Degree of freedom : df = 49 [ df=n-1]

Significance level :
$\alpha=1-0.95=0.05$

Using students's t-distribution table, the critical t-value for 95% confidence =
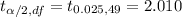
$t_(\alpha/2,df)=t_(0.025,49)=2.010$

Then, 95% confidence interval for the population mean will be :

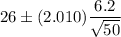
$26\pm (2.010)(6.2)/(√(50))$

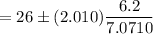
$=26\pm (2.010)(6.2)/(7.0710)$

$=26\pm (2.010)(0.87682)$

$\approx26\pm1.76$

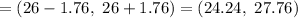
$=(26-1.76,\ 26+1.76)=(24.24,\ 27.76)$

Hence, a 95% confidence interval for the population mean = (24.24, 27.76)

Since 28 is not contained in the above confidence interval , it means it is not reasonable that the population mean is 28 weeks.