Question

The midpoint M of CD has coordinates (2, 5). Point C has coordinates (4, 3). What are the coordinates of point D?

Answer 1

The coordinates of point D is (0, 7)

solution:

The midpoint M of CD has coordinates (2, 5)

Point C has coordinates (4, 3)

To find: coordinates of point D

The midpoint of line AB conatining points
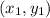`(x_1, y_1)` and
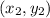`(x_2, y_2)` is given as:

`\text {midpoint}(x, y)=\left((x_(1)+x_(2))/(2), (y_(1)+y_(2))/(2)\right)`

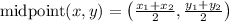
Here in this problem,

Midpoint (C, D) = (2, 5)

`point C (x_1, y_1) = (4, 3)`

`\text {point } D\left(x_(2), y_(2)\right)=?`

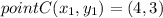
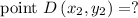
Subsituting the values in formula we get,

`(2,5)=\left((4+x_(2))/(2), (3+y_(2))/(2)\right)`

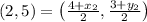
On comparing both the sides we get,

`2=(4+x_(2))/(2) \text { and } 5=(3+y_(2))/(2)`

`\begin{array}{l}{4=4+x_(2) \text { and } 10=3+y_(2)} \\\\ {\text {Therefore } x_(2)=0 \text { and } y_(2)=7}\end{array}`

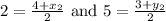
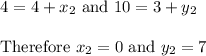
Thus the coordinates of point D is (0, 7)