The coordinates of point D is (0, 7)
solution:
The midpoint M of CD has coordinates (2, 5)
Point C has coordinates (4, 3)
To find: coordinates of point D
The midpoint of line AB conatining points
 and
and
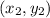 is given as:
is given as:
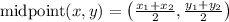
Here in this problem,
Midpoint (C, D) = (2, 5)
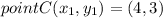
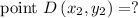
Subsituting the values in formula we get,
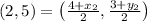
On comparing both the sides we get,
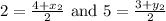
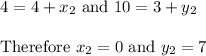
Thus the coordinates of point D is (0, 7)