Question

Justin has two coupons for a phone.

Coupon A: $45 rebate on a $65 phone
Coupon B: 65% off of a $65 phone
Choose the coupon that gives the lower price.
Then fill in the blank with the correct value.
Coupon A gives the lower price.
The price with coupon A is less than the price with coupon B.
• Coupon B gives the lower price.
The price with coupon B is $ less than the price with coupon A.

Answer 1

Coupon A: $45 rebate on a $65 phone. $2.75

Explanation:

We want to find out which coupon gives the lower price.

Finding the price with coupon A:

Coupon A is for a $45 rebate on a $65 phone.

A rebate is a discount. It is an amount subtracted from the full price.

So to find the price with coupon A, we subtract.

65-45=$20

The price with coupon A is $20.

Finding the price with coupon B:

Using coupon B, Justin gets 65% off of a $65 phone.

To find 65% of $65, we first change 65% to a decimal, and then multiply.

65% of 65=0.65 × 65 = $42.25

So the discount with coupon B is $42.25

To find the price with coupon B, we subtract.

65.00 - 42.25 = $22.75.

So the price with coupon A is $2.75 less then the price with coupon B.

Answer 2

1) Coupon A gives the lower price.

The price with coupon A is less than the price with coupon B.

Explanation:

Here, according to the given details:

Coupon A : $45 rebate on $65 phone

So, the actual paid price for phone = $65 - $45 = $20

If we apply Coupon A , the cost of the phone = $20

Coupon B : 65% off on $65 phone

Now, calculating 65% of 65, we get:

`(65)/(100)  * 65 = 42.25`

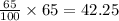
So, the discounted amt on $65 phone is $42,25

So, the actual paid price for phone = $65 - $42.25 = $22.75

If we apply Coupon B , the cost of the phone = $22.75

Hence, Coupon A gives the lower price.

The price with coupon A is less than the price with coupon B.